http://docs.mongodb.org/manual/reference/sql-aggregation-comparison/
Monthly Archives: December 2014
Ugly Numbers Program
Ugly numbers are numbers whose only prime factors are 2, 3 or 5. The sequence
1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, …
shows the first 11 ugly numbers. By convention, 1 is included.
Write a program to find and print the 150’th ugly number.
# include
# include
/*This function divides a by greatest divisible
power of b*/
int maxDivide(int a, int b)
{
while (a%b == 0)
a = a/b;
return a;
}
/* Function to check if a number is ugly or not */
int isUgly(int no)
{
no = maxDivide(no, 2);
no = maxDivide(no, 3);
no = maxDivide(no, 5);
return (no == 1)? 1 : 0;
}
/* Function to get the nth ugly number*/
int getNthUglyNo(int n)
{
int i = 1;
int count = 1; /* ugly number count */
/*Check for all integers untill ugly count
becomes n*/
while (n > count)
{
i++;
if (isUgly(i))
count++;
}
return i;
}
/* Driver program to test above functions */
int main()
{
unsigned no = getNthUglyNo(150);
printf("150th ugly no. is %d ", no);
getchar();
return 0;
}
This method is not time efficient as it checks for all integers until ugly number count becomes n, but space complexity of this method is O(1)
Methods to use involve dynamic programming, google it
Java Inner Classes
Pendrive dosent show files even though storage is occupied
Check if the files are not in hidden mode.
Click on “Start” –>Run –> Type cmd and press Enter.
Here I assume your pendrive drive letter as G:
Enter this command.
attrib -h -r -s /s /d g:\*.* –> Press Enter
You can copy the above command –> Right-click in the Command Prompt and
paste it.
Note : Replace the letter g with your pen drive letter.
Now check your pen drive for the files.
What is Deadlock ?
- Program 1 requests resource A and receives it.
- Program 2 requests resource B and receives it.
- Program 1 requests resource B and is queued up, pending the release of B.
- Program 2 requests resource A and is queued up, pending the release of A.
Program to print all permutations of a given string(Backers Algorithm)
Below are the permutations of string ABC.
ABC, ACB, BAC, BCA, CAB, CBA
Here is a solution using backtracking.
public class TestClass {
public static void main(String[] args) {
char a[] = new char[3];
a[0] = 'A';
a[1] = 'B';
a[2] = 'C';
permute(a, 0, a.length-1);
}
/* Function to print permutations of string
This function takes three parameters:
1. String
2. Starting index of the string
3. Ending index of the string. */
public static void permute(char[] a, int i, int n)
{
int j;
if (i == n)
System.out.println(a);
else
{
for (j = i; j <= n; j++)
{
a = swap(a,i,j);
permute(a, i+1, n);
a = swap(a,i,j); //backtrack
}
}
}
public static char[] swap (char[] a,int index0,int index1 )
{
char temp;
temp = a[index0];
a[index0] = a[index1];
a[index1] = temp;
return a;
}
}
Permutations and Combinations
Quick Formula :
- Permutations with Repetition : nr
- Permutations without Repetition :
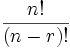
- Combinations with Repetition :
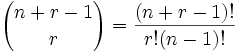
- Combinations without Repetition :
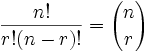
Permutations
There are basically two types of permutation:
- Repetition is Allowed: such as the lock above. It could be “333”.
- No Repetition: for example the first three people in a running race. You can’t be first and second.
1. Permutations with Repetition
These are the easiest to calculate.
When we have n things to choose from … we have n choices each time!
When choosing r of them, the permutations are:
n × n × … (r times)
n × n × … (r times) = nr
So, the formula is simply:
| nr |
| where n is the number of things to choose from, and we choose r of them (Repetition allowed, order matters) |
2. Permutations without Repetition
In this case, we have to reduce the number of available choices each time.
For example, what order could 16 pool balls be in?
After choosing, say, number “14” we can’t choose it again.
So, our first choice has 16 possibilites, and our next choice has 15 possibilities, then 14, 13, etc. And the total permutations are:
16 × 15 × 14 × 13 × … = 20,922,789,888,000
But maybe we don’t want to choose them all, just 3 of them, so that is only:
16 × 15 × 14 = 3,360
The formula is written:
| |
Combinations
There are also two types of combinations (remember the order does not matter now):
- Repetition is Allowed: such as coins in your pocket (5,5,5,10,10)
- No Repetition: such as lottery numbers (2,14,15,27,30,33)
2. Combinations without Repetition
This is how lotteries work. The numbers are drawn one at a time, and if we have the lucky numbers (no matter what order) we win!
The easiest way to explain it is to:
- assume that the order does matter (ie permutations),
- then alter it so the order does not matter.
Going back to our pool ball example, let’s say we just want to know which 3 pool balls are chosen, not the order.
We already know that 3 out of 16 gave us 3,360 permutations.
But many of those are the same to us now, because we don’t care what order!
For example, let us say balls 1, 2 and 3 are chosen. These are the possibilites:
| Order does matter | Order doesn’t matter |
| 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 |
1 2 3 |
So, the permutations will have 6 times as many possibilites.
In fact there is an easy way to work out how many ways “1 2 3” could be placed in order, and we have already talked about it. The answer is:
3! = 3 × 2 × 1 = 6
(Another example: 4 things can be placed in 4! = 4 × 3 × 2 × 1 = 24 different ways, try it for yourself!)
So we adjust our permutations formula to reduce it by how many ways the objects could be in order (because we aren’t interested in their order any more):
![]()
That formula is so important it is often just written in big parentheses like this:
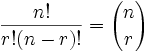 |
1. Combinations with Repetition
OK, now we can tackle this one …
Let us say there are five flavors of icecream: banana, chocolate, lemon, strawberry and vanilla.
We can have three scoops. How many variations will there be?
Let’s use letters for the flavors: {b, c, l, s, v}. Example selections include
- {c, c, c} (3 scoops of chocolate)
- {b, l, v} (one each of banana, lemon and vanilla)
- {b, v, v} (one of banana, two of vanilla)
(And just to be clear: There are n=5 things to choose from, and we choose r=3 of them.
Order does not matter, and we can repeat!)
This is like saying “we have r + (n-1) pool balls and want to choose r of them”. In other words it is now like the pool balls question, but with slightly changed numbers. And we can write it like this:
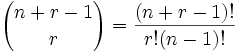 |
A Beginner’s Guide to Big O Notation
Big O notation is used in Computer Science to describe the performance or complexity of an algorithm. Big O specifically describes the worst-case scenario, and can be used to describe the execution time required or the space used (e.g. in memory or on disk) by an algorithm.
Anyone who’s read Programming Pearls or any other Computer Science books and doesn’t have a grounding in Mathematics will have hit a wall when they reached chapters that mention O(N log N) or other seemingly crazy syntax. Hopefully this article will help you gain an understanding of the basics of Big O and Logarithms.
As a programmer first and a mathematician second (or maybe third or fourth) I found the best way to understand Big O thoroughly was to produce some examples in code. So, below are some common orders of growth along with descriptions and examples where possible.
O(1)
O(1) describes an algorithm that will always execute in the same time (or space) regardless of the size of the input data set.
bool IsFirstElementNull(String[] strings)
{
if(strings[0] == null)
{
return true;
}
return false;
}
O(N)
O(N) describes an algorithm whose performance will grow linearly and in direct proportion to the size of the input data set. The example below also demonstrates how Big O favours the worst-case performance scenario; a matching string could be found during any iteration of the for loop and the function would return early, but Big O notation will always assume the upper limit where the algorithm will perform the maximum number of iterations.
bool ContainsValue(String[] strings, String value)
{
for(int i = 0; i < strings.Length; i++)
{
if(strings[i] == value)
{
return true;
}
}
return false;
}
O(N2)
O(N2) represents an algorithm whose performance is directly proportional to the square of the size of the input data set. This is common with algorithms that involve nested iterations over the data set. Deeper nested iterations will result in O(N3), O(N4) etc.
bool ContainsDuplicates(String[] strings)
{
for(int i = 0; i < strings.Length; i++)
{
for(int j = 0; j < strings.Length; j++)
{
if(i == j) // Don't compare with self
{
continue;
}
if(strings[i] == strings[j])
{
return true;
}
}
}
return false;
}
O(2N)
O(2N) denotes an algorithm whose growth will double with each additional element in the input data set. The execution time of an O(2N) function will quickly become very large.
Logarithms
Logarithms are slightly trickier to explain so I’ll use a common example:
Binary search is a technique used to search sorted data sets. It works by selecting the middle element of the data set, essentially the median, and compares it against a target value. If the values match it will return success. If the target value is higher than the value of the probe element it will take the upper half of the data set and perform the same operation against it. Likewise, if the target value is lower than the value of the probe element it will perform the operation against the lower half. It will continue to halve the data set with each iteration until the value has been found or until it can no longer split the data set.
This type of algorithm is described as O(log N). The iterative halving of data sets described in the binary search example produces a growth curve that peaks at the beginning and slowly flattens out as the size of the data sets increase e.g. an input data set containing 10 items takes one second to complete, a data set containing 100 items takes two seconds, and a data set containing 1000 items will take three seconds. Doubling the size of the input data set has little effect on its growth as after a single iteration of the algorithm the data set will be halved and therefore on a par with an input data set half the size. This makes algorithms like binary search extremely efficient when dealing with large da
